The Case of the Missing Increment

An innocent single-cycle loop test leads to a surprising microarchitecture discovery

Computer Enhance was never meant to be a place for publishing novel investigations into software performance, but sometimes it happens by accident. We already saw this once when bonus materials for the Performance-Aware Programming course lead us to discover a previously undocumented 16-ahead mapping pattern in the Windows memory manager.

In that same vein, on a specific set of Intel CPUs, some of our tutorial loops hit a mostly undocumented performance anomaly in the Golden Cove microarchitecture. I say “mostly” because — SPOILER WARNING — once I figured out what was happening, I was able to search for and find a single solitary hint about it in a writeup of one of Intel’s Architecture Day presentations.

But I’m getting ahead of myself.

It Was Supposed To Be Simple

The scene of this particular whodunnit may seem unlikely: the performance anomaly occurs in some of the simplest machine code we could consider. In fact, you might say it’s oversimplified code, since it doesn’t do any useful work. It’s entire raison d'être was illustrating hardware behavior for educational purposes.

But in my experience, extremely simple machine code is actually one of the most common places to witness something strange. Since you’re handing the CPU a few highly-specific instructions without most of the code that would otherwise be interleaved, you’re pushing the boundaries of what its designers expected to encounter in real use. At this point, you’re more likely — not less — to feel the edges of the microarchitecture than you are in a more typical scenario.

The specific oversimplified code that kicks off our mystery comes from the course’s introductory video on how to link to ASM files for microbenchmarking. It wasn’t even a performance exploration!

But that’s fortunate for our purposes, because even if you haven’t taken Part I of the course yet, and don’t know how to read assembly language, the source code is simple enough that you can probably understand what it does anyway:

.loop:
    inc rax
    cmp rax, rcx
    jb .loop

This loop consists of just three instructions. In higher-level-language terminology, the first instruction — inc rax — adds one to a variable. The second — cmp rax, rcx — determines if that variable is less than the desired iteration count¹. And the third — jb .loop — repeats the loop if it was.

In a higher-level language, you might write the same loop like this:

do {                // .loop
    i++;            // inc rax
} while(i < count); // cmp rax, rcx combined with jb .loop

Any x64 chip can run this loop. It does not involve any fancy instructions from the AVX or AVX-512 instruction sets that might only exist on newer processors. In fact, it’s almost simple enough to run on the original 8086/88! The only thing preventing it from assembling to 8086 code is that it happens to use 64-bit registers instead of 16-bit registers. Change the rax and rcx to ax and cx and it would assemble to valid 8086 code.

What’s more, not only is the loop itself simple to understand, but if you know some modern microarchitecture basics, its performance is easy to understand — or at least, it would have been, if it weren’t for the anomaly we’re about to discuss.

There is a subtlety regarding inc rax and how the flags are updated, but it doesn’t actually affect this particular analysis, so you don’t need to know it to understand the mystery. In fact, flags are not really important here, so I will be omitting the flags tracking in the following breakdowns so they are easier to read. But please keep in mind that of course there are flags being generated and tracked through this loop, so if this were a scenario where flag operations affected the outcome, you would have to consider that.

That caveat aside, assuming we feed this loop a sufficiently high value for rcx (the count), the jump back to the top of the loop will occur the vast majority of the time. Only on the very last iteration will it fall through to the next block of code. This means the front-end of the CPU should correctly predict the repetition and feed the back-end a repeating series of microoperations that effectively encode this² (not counting the flag writes, as I just mentioned):

    rax <- rax + 1
    cmp rax, rcx / jb
    rax <- rax + 1
    cmp rax, rcx / jb
    rax <- rax + 1
    cmp rax, rcx / jb
    rax <- rax + 1
    cmp rax, rcx / jb
    ...

Since register names are just that — names — the renaming stage will turn this into something conceptually similar to Single Static Assignment form:

    g2 <- g1 + 1
    cmp g2, g0 / jb
    g3 <- g2 + 1
    cmp g3, g0 / jb
    g4 <- g3 + 1
    cmp g4, g0 / jb
    g5 <- g4 + 1
    cmp g5, g0 / jb
    ...

where the numbered g’s are register file entries for general purpose registers. Since rcx (here depicted as residing in g0) does not change, the dependency structure for this loop is entirely based on the increment. For every increment, there is a pair of microoperations that must wait for it to complete, one of which is the next increment:

    g2 <- g1 + 1

    // Must wait for g2
    cmp g2, g0 / jb
    g3 <- g2 + 1

    // Must wait for g3
    cmp g3, g0 / jb
    g4 <- g3 + 1

    // Must wait for g4
    cmp g4, g0 / jb
    g5 <- g4 + 1

    // Must wait for g5
    cmp g5, g0 / jb
    ...

This leads us to our straightforward steady-state expectation for the performance of this loop. Because the back-end must wait for the result of a previous increment before performing each pair of dependent microoperations, and the fastest possible delivery of a result is one core clock cycle, we would expect this loop to have a maximum throughput of one core clock cycle per iteration.

So, for example, if we have a processor with a boost clock of 5GHz, we would expect it perform no more than five billion iterations of this loop per second: one iteration for every core clock cycle it observes.

If we measure the performance of this loop on a variety of x64 microarchitectures, we get exactly the performance we expect. The Skylake, Zen 2, and Zen 4 processors we have here at the office all run this loop at one cycle per iteration when measured.

Furthermore, if we run simulations of this loop using the best publicly available Intel microarchitecture simulator, the simulator predicts it will take one cycle for each iteration on every Intel architecture it supports: Sandy Bridge, Ivy Bridge, Haswell, Broadwell, Skylake, Skylake-X, Kaby Lake, Coffee Lake, Cascade Lake, Ice Lake, Tiger Lake, and Rocket Lake.

Everything checks out. So what’s the problem?

The Alder Lake Anomaly

As I learned 20+ years ago at RAD Game Tools, you learn about all sorts of weird PC hardware anomalies when you ship to a wide audience. Unless you have regular access to a massive testing lab covering thousands of combinations of PC hardware, there’s no way you can foresee some of the crazy things that happen in the wild. So I fully expected to have a few weird things come up when people in the Performance-Aware Programming course started doing their own microbenchmarking.

So far, there have only been two: one is an as-yet-uninvestigated Kaby Lake memory throughput anomaly³, and the other is the Alder Lake performance of the loop I described in the previous section.

Specifically, the machine I used to reproduce the anomaly was an i7-12700K. This is an Alder Lake processor with a maximum boost clock of 5GHz. Following the logic from the previous section, if you run our simple inc/cmp/jb loop on this processor, it should max out at five billion iterations per second — again, one core cycle for every iteration. Based on our analysis, we would expect anything more than that to be both practically and theoretically impossible on this processor.

By basic math, we can also say the theoretical maximum for any number of iterations. Three billion iterations should take three billion cycles. Two billion iterations? Two billion cycles. And so on.

In the particular case we tested in the course, we were running 1,073,741,824 iterations. While that may seem like an oddly specific number, it’s just the number of bytes in a gigabyte of memory (2^30, or 1024*1024*1024, or however you’d like to think of it).

When run on my Skylake processor with boost clock disabled, this test took 1,074,730,560 cycles as measured by the chip-wide timestamp counter (read via rdtsc). This unavoidably includes a little bit of inaccuracy at the edges, since normally execution is highly overlapped, so it’s hard to declare a performance measurement in isolation. But even so, the results line up extremely well with our expectations: 1,074,730,560 cycles divided by 1,073,741,824 iterations is approximately 1.0009 cycles per iteration — very close to 1.

However, when run on the Alder Lake i7-12700K, we get something rather different: the timestamp counter reports only 391,416,518 cycles elapsed. 391,416,518 cycles divided by 1,073,741,824 iterations is 0.364535 cycles per iteration — that’s 2.7x faster than should be theoretically possible!

At first glance, this is not immediately concerning. If you’ve done a lot of microbenchmarking before, you know that on modern chips the rdtsc-read timestamp counter counts cycles at the base clock rate and does not account for things like single-core clock boosting. So your first thought is probably “the boost clock must be around three times the base clock on this processor”.

But is it? That seems like a pretty high boost clock ratio, no?

If we look back at the spec sheet, we find that the base clock is 3.60GHz for the P-cores and 2.70GHz for the E-cores, while the max boost clock is 5.00GHz for the P-cores, and 3.80GHz for the E-cores. In order for there to be a 2.7x multiplier between the base clock and the boost clock, even taking the maximum boost of 5Ghz, we would expect a base clock value of around 1.8Ghz — nowhere near even the E-core base clock, let alone the P-core base clock.

What’s more, if you actually measure the number of timestamp counter cycles that occur in one second as observed by the core running the test, you get right around 3.6GHz. So we more-or-less know that we’re running on a P-core, that its TSC is running at 3.6GHz, and that the maximum multiplier we would expect from boosting is therefore 5GHz/3.6GHz.

Unfortunately, that’s 1.4x — approximately half of the 2.7x observed in practice.

The Ultimate Sadness

So even taking the boost clock into account, we have no way to explain this anomaly. Just to throw the ratios at you one other way, for our 1,073,741,824 iterations we are seeing 391,416,518 timestamps elapse out of 3,600,000,000 each second. That means the test is taking 0.108727 seconds total. If the CPU were in fact taking 1 (boosted) core cycle per iteration at 5GHz, that would be 1,073,741,824 core cycles out of 5,000,000,000 each second, or 0.214748 seconds.

In other words, at max boost, we would expect our test to take 0.214748 seconds, but it only takes 0.108727 seconds when we measure it. That’s double the predicted performance. Unless we’ve done something wrong, Alder Lake appears to run our loop at twice the theoretical maximum!

That simply can’t be right, can it? I don’t know about you, but I certainly assumed it couldn’t be, As a Windows developer, that made me feel a certain sense of dread, because at that point, I had the sinking feeling I might once again be forced to experience… The Ultimate Sadness.

For those who don’t know, The Ultimate Sadness is the category of programming tasks that involve things like being forced to use XML as a data format. It’s that moment when you have a programming problem that would be trivial to solve if the underlying substrate was sane, but instead it seems as if someone designed it specifically to make your life miserable.

In this particular case, the substrate in question is Event Tracing for Windows, AKA the worst API ever made.

The reason Windows developers often look at performance using bare rdtsc readings isn’t because that’s the best way to measure things. rdtsc on modern processors is really just a glorified wall clock. We would much prefer to employ the whole suite of detailed performance monitoring counters (or “PMCs” for short) present in modern x64 chips.

But as Windows developers, we usually don’t, because stock Windows makes it a massive pain in the butt to read them. While rdtsc⁴ is convenient to call at any time from a user-level application, there is no similarly convenient way for a user-level application to read a whole host of other valuable PMCs offered by x64 processors.

Broadly speaking, Windows developers only get three options:

1. Install a third-party suite that comes with a kernel-level driver for PMC collection (VTune, Intel Performance Counter Monitor, etc.)

2. Port to an environment that has better native PMC access (Linux, direct boot from BIOS, etc.)

3. Suffer The Ultimate Sadness that is Event Tracing for Windows, either by directly calling the API, or using some combination of front-end tools (wpr, xperf, tracelog, etc.)

No matter what option you pick, you’re looking at something substantially more annoying than the ten seconds it takes to type __rdtsc() into your code⁵. Since the only Alder Lake machine I had access to was a remote Windows machine that didn’t belong to me, I more-or-less had to choose option 3, which meant subjecting myself to The Ultimate Sadness.

In an effort to avoid spreading The Ultimate Sadness to all of you, I’ll spare you the gory details and get right to the data. Using the needlessly-limited functionality of ETW, we can indirectly collect two additional PMC counters that will give us a more precise picture of what is going on when Alder Lake runs this loop.

The first counter is exposed as “TotalIssues” by ETW, and counts the number of instructions a core believes it has issued. The second counter is exposed as “UnhaltedCoreCycles” — or equivalently for this purpose we could use the PMC exposed under the ETW name “TotalCycles” — and counts the number of clock cycles the core itself has gone through (not the invariant TSC cycles, but the core’s actual cycles, including boosting).

If we collect these counters while running our loop on my boost-disabled Skylake, we get deltas in line with what we expect:

1073970036 TSC elapsed / 1073741824 iterations [0 switches]
  3221373030 TotalIssues
  1073970333 TotalCycles
  1073970331 UnhaltedCoreCycles

The number of cycles observed by the core is approximately equal to the number of timestamps (TSC) elapsed, just like we expect when the core is not allowed to boost. The number of instructions issued is roughly three times (~2.999500x) the number of cycles observed, which is also what we expect if each iteration took one cycle: there are three instructions in the loop, so if on average they execute in one cycle, there should be three issues per cycle.

But what happens if we collect the same counters from the Alder Lake machine?

388096288 TSC elapsed / 1073741824 iterations [0 switches]
  3221327798 TotalIssues
   536959840 TotalCycles
   536959830 UnhaltedCoreCycles

Unlike the Skylake machine, the TSC elapsed differs from the cycles elapsed, but that’s expected since we haven’t disabled boost on this machine. The ratio of cycles to TSCs is ~1.383573x, which is right in line with the expected maximum boost clock ratio of 5.0GHz vs. 3.6GHz (~1.388889x). So our PMC collection certainly seems correct, and confirms that something close to the maximum boost clock is kicking in — no surprises there.

But then we get to the “TotalIssues” number. Again, the theoretical maximum issues per cycle for this loop should be three, and it was three on Skylake.

Here on Alder Lake, however, we get 3,221,327,798 issues in 536,959,840 core cycles — an issue rate of six instructions per cycle (~5.999197x). Instead of disproving our previous results, this appears to completely confirm them: according to the PMCs, Alder Lake really is processing two iterations of our loop every core clock cycle.

Unless it’s just straight-up lying, the core is legitimately operating at double the expected maximum throughput.

Can This Possibly Be Right?

Alder Lake P-cores use a microarchitecture Intel calls Golden Cove. Since we’re clearly observing the loop run at a boost clock near 5GHz, there is no doubt the measurements we’re taking are on one of these Golden Cove P-cores, not one of the less-powerful E-cores.

In one limited sense, then, our results aren’t surprising: Golden Cove cores are supposed to be able to execute six instructions per cycle. That’s their theoretical maximum instruction throughput. So at least the core isn’t violating its basic operating parameters as stated by Intel.

But in the broader sense, these results are rather surprising. Unless I made a serious error in collecting the data — which is always a possibility with delicate testing like this — we now have proof that a Golden Cove core can perform two serially dependent increments on a single clock cycle. While in theory there’s no reason a core couldn’t have sufficient logic to produce that result, I did not know that was possible on any x64 core until this experience.

Specifically, a sustained throughput of 6 instructions per cycle for this loop means that 2 of those 6 instructions are increments of rax:

inc rax ; [A]
inc rax ; [B]

Again, written out more explicitly, that would be:

g2 <- g1 + 1 ; [A]
g3 <- g2 + 1 ; [B]

Normally, to execute [B], the result g2 has to be forwarded from the execution unit computing [A] to the execution unit that will compute [B], because [B] requires g2 as an input and it is not known until [A] computes it. This is why we expect to wait at least one cycle per increment: it should take at least that long to compute and forward the result from the previous increment.

However, we are clearly seeing both [A] and [B] complete in the same cycle. Something very unexpected is happening here.

All of the computation-unit-based explanations I could think of would be extraordinarily weird and probably can’t be true. These would be nonsense explanations like the adder ALUs and scheduler having a magic mode where they operate twice in one clock cycle; two ALUs being combined to do one double-increment while optionally writing back two sets of flags; the core boosting to 10GHz but the PMCs still cap at 5GHz for some other reason; etc.

I’m not a hardware designer, so my imagination is quite limited here. Maybe there are more obvious ways you would do this that I just don’t know. But, unless there are, I don’t see a simple explanation for how the scheduling and execution parts of the core could produce this result by themselves.

Which leaves the front-end and the rename/elimination parts of the core. Here, I was able to come up with an explanation that wasn’t completely ridiculous.

The idea is that perhaps, without making a big deal about it, Intel added the ability for the rename stage itself to adjust immediate addition operations in order to remove dependencies. If that were the case, it would be possible, pre-scheduling, for the core to rewrite this:

inc rax ; [A]
inc rax ; [B]

not only in the way we would normally expect:

g2 <- g1 + 1 ; [A]
g3 <- g2 + 1 ; [B]

but also optionally in a less-dependent form:

g2 <- g1 + 1     ; [A]
g3 <- (g1+1) + 1 ; [B]

This way, instead of only one increment becoming ready to execute on production of a result, two become ready instead. As soon as g1 is computed, both [A] and [B] can begin executing, instead of [B] stalling until [A] completes.

Furthermore, it seems plausible that — if this feature were restricted to operating between two or more add-immediate instructions — it could be done entirely at rename time just by altering the constants. Thanks to associativity, the renamer could reassociate this:

g3 <- (g1+1) + 1 ; [B]

like this:

g3 <- g1 + (1 + 1) ; [B]

which simplifies to this:

g3 <- g1 + 2 ; [B]

That would be no more difficult to represent in the pipeline than any other immediate addition. Nothing downstream of the renamer would have to change.

I have no idea how plausible any of this is, but it at least sounds plausible to me, which is more than I can say for any other explanation I came up with.

Possible Confirmation from Intel

Armed with both a reasonable certainty that the CPU was sustaining two iterations per core clock cycle, and a plausible theory about how that might happen, I tried again to find a documentation of this Golden Cove capability somewhere.

I’d also done this at the outset, of course, but found nothing. The Agner Fog microarchitecture manual doesn’t mention anything like this, and doesn’t seem to cover Golden Cove in much detail. The Intel optimization manual does list a number of enhancements for Golden Cove, but doesn’t mention anything like this.

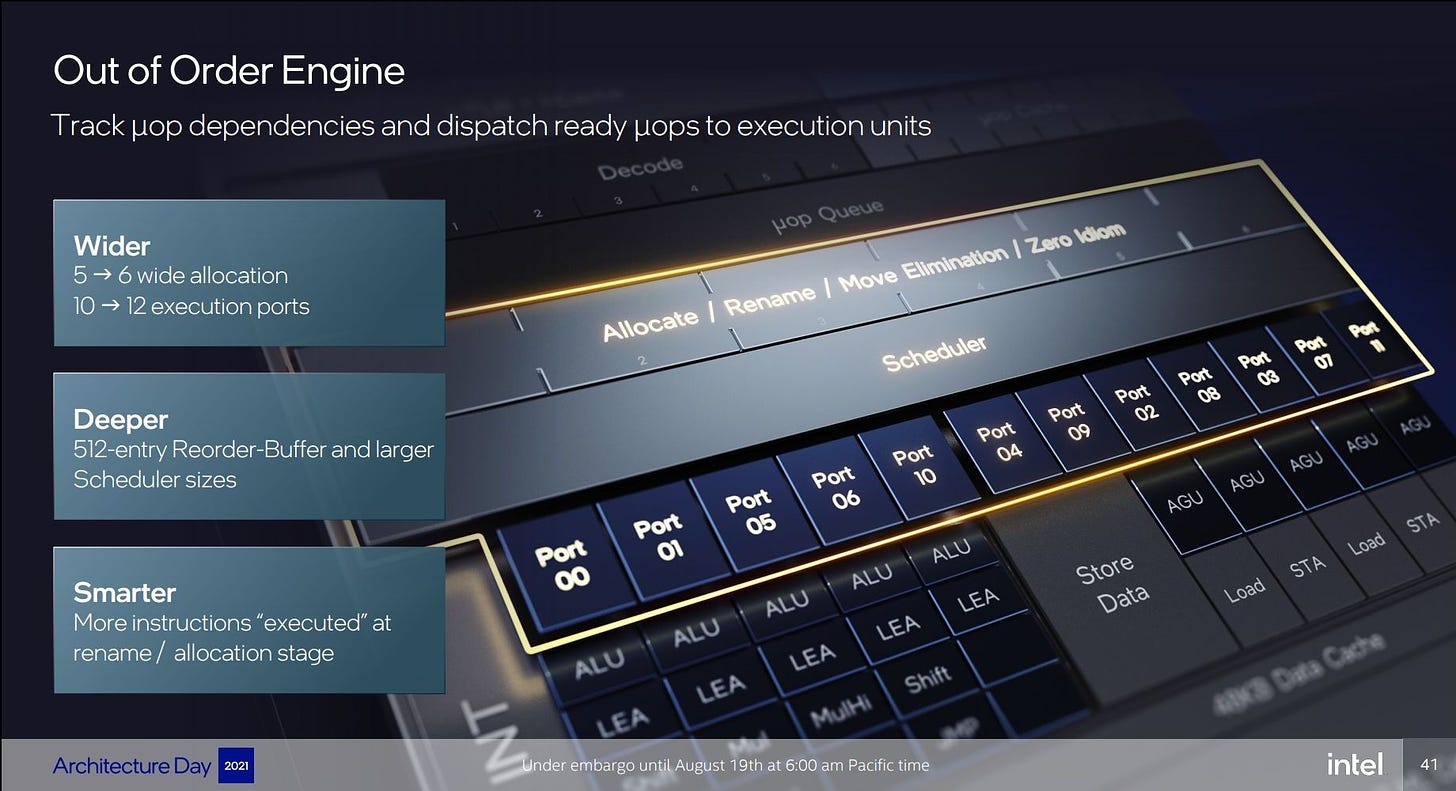
However, once I suspected I was looking for something involving optimized immediate addition, after a fair bit of search term juggling I was finally able to find one — yes, just one — possible confirmation that my theory is correct. It comes from an AnandTech⁶ writeup of a slide presentation Intel gave on one of their “Architecture Days”. It appears to be downstream of the following slide, where the “Smarter” box claims that more instructions are “executed” at the “rename / allocation” stage:

While that doesn’t really tell us much, AnandTech must have received information from Intel privately afterward — or seen some additional public disclosure that I haven’t been able to find — because they included this more detailed elaboration in their writeup:

From this article on AnandTech.

Unfortunately, I still have no idea where they got this information. I went back and watched the Architecture Day video myself, and all the presenter says is what’s written on the slide: some instructions are now “executed” at the rename / allocation stage.

Given the ambiguity here, I would consider this mystery mostly solved, but not quite. We now know essentially what is happening, and why. But since I can’t find a complete description of how this new feature works, a piece of the puzzle remains missing.

Specifically, AnandTech used the phrase “treated as NOPs”. If that’s accurate, then the hypothetical mechanism I described might not be correct. My proposed method doesn’t eliminate the immediate additions — it just rebalances them to shorten the length of dependency chains. In my hypothetical model, this:

inc rax
inc rax
inc rax
inc rax

at best becomes this:

g2 <- g1 + 1
g3 <- g1 + 2
g4 <- g1 + 3
g5 <- g1 + 4

which is still 4 micro-operations — the same number it would have taken without the immediate folding. The benefit is solely that all four micro-ops can now run in parallel, whereas previously they would have had to be serialized. At no point did any increment turn into a NOP!

Of course, it’s possible that both my hypothesis and AnandTech’s statement are true. The reference to NOPs could be talking about a subsequent step that happens after the step I proposed. If the allocator notices that a register name has been overwritten, and the result of a not-yet-scheduling addition can therefore never be referenced, it could perform a kind of dead-code elimination and discard the operation ahead of time.

For example, in the four-micro-op sequence above, if there were no uses of rax in-between increments, then as it renamed the incs it could notice that the results of the g2, then g3, then g4 micro-ops could never be used. If it noticed this early enough, it could discard some of them before ever sending them to the scheduling queues.

That might be plausible, but, I’m way outside my area of expertise here. I’m really just guessing. I do software, not hardware, so I would much prefer to find some actual documentation on this new microarchitectural feature!

Absent that, I do think it would be possible to construct a series of microbenchmarks — hopefully using Linux so one could get easier and more extensive PMC access — that taken together would suggest what’s going on internally. It’s not hard to imagine feeding Golden Cove a series of slightly different instruction sequences to see exactly what it can and can’t do with immediate additions.

Unfortunately, that process would require permanent access to an Alder Lake machine, which I do not have. So, sadly, it will have to fall to someone else out there who likes poking at x64 cores!

If you enjoyed this article, and would like to receive more like it, you can put your email address in the box below to access both our free and paid subscription options:

Special Thanks

I would once again like to thank Mārtiņš Možeiko’s for fearlessly producing great reference material for some of the world’s most finicky tools and APIs. While investigating this anomaly, I wrote some new profiling code that streamlined the process of collecting PMCs from ETW. In doing so, I was helped tremendously by Mārtiņš miniperf reference code. ETW is incredibly flakey, and often fails to work for undocumented or convoluted system configuration reasons. Having miniperf to work from and check against was of the few things that allowed me to stay (mostly) sane in the process.

1. Technically, since it sets several flags, it can determine multiple things about the relationship between the two inputs — but we’re only going to use it as a “less than” in the following conditional jump.

2. How exactly the jb gets processed is not typically documented, but microarchitecture manuals often describe it as being “fused” with the cmp during at least part of the pipeline, meaning that the internal representation of the cmp and jb travel as a unit through the queues rather than being treated as completely separate microoperations. I have notated the fused jb as “/ jb” everywhere, even though at some point it may become “unfused” for separate processing — specifically, the eventual check to see if the branch prediction was correct. Since it does not matter for purposes of the rudimentary performance explanation, in the informal notation used in the article I did not attempt to represent if/when separate processing of the jb might happen.

3. The reason I have not investigated the Kaby Lake anomaly yet is because, despite many attempts to contact Intel for access to a Kaby Lake machine, I have been unable to establish a relationship with them for this purpose. The only reason I was able to investigate the Alder Lake anomaly discussed in this article is because one of the people taking the course set up a remote desktop connection for me to their own machine.

4. And more recently on AMD hardware, rdpru, which I absolutely love — thank you AMD!

5. Which, by the way, is how easy it is to insert PMC monitoring into the actual machine code. One you select the PMCs you want, you can read a PMC with a single rdpmc instruction, just like you read the TSC with the rdtsc instruction. So the only reason we can’t read PMCs with a simple intrinsic is because Windows specifically prevents us from doing so, largely for security reasons — and that would be fine if it then provided a sane API for accessing PMCs, which of course it doesn’t.

6. Rest in peace :(